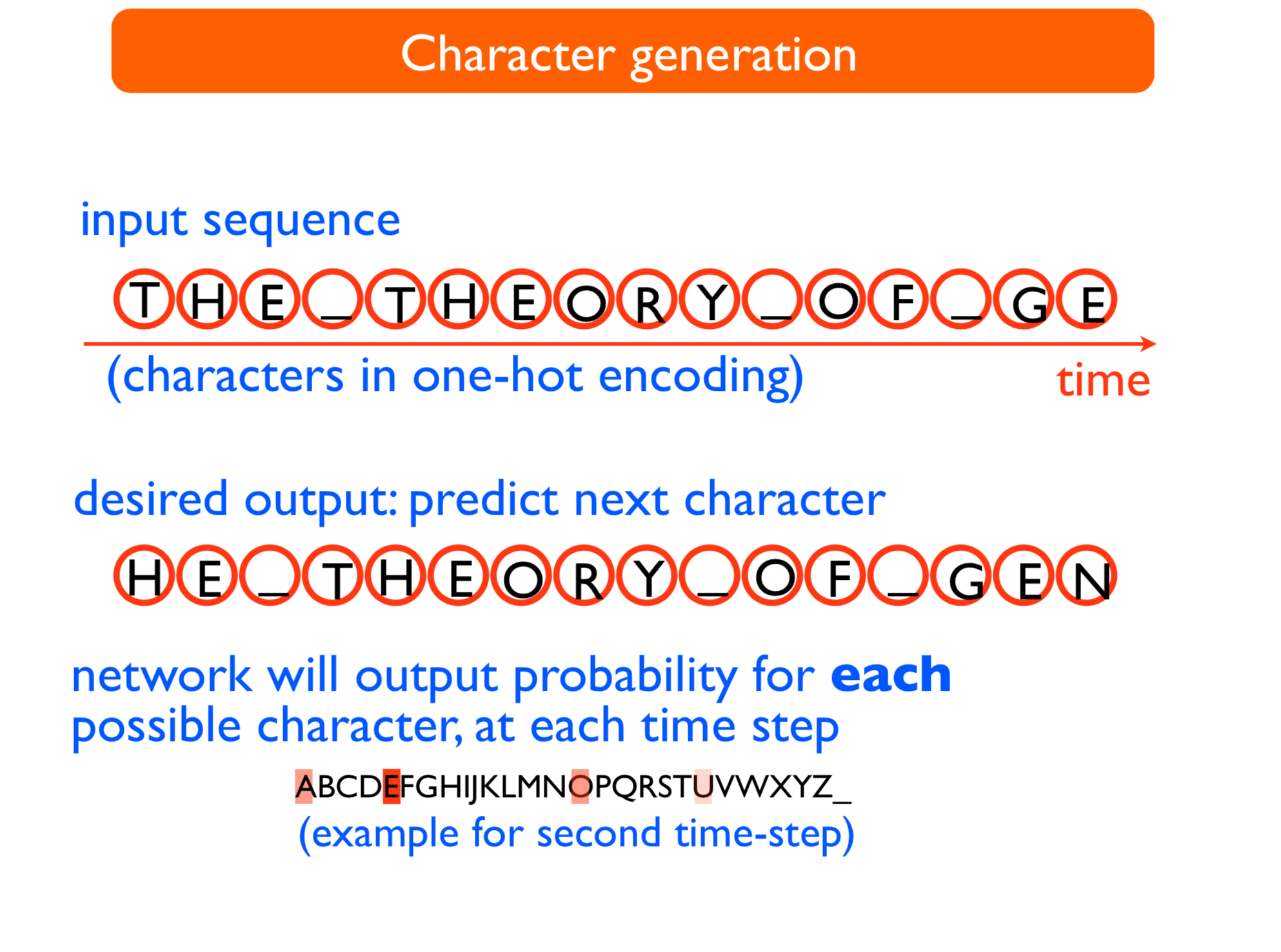
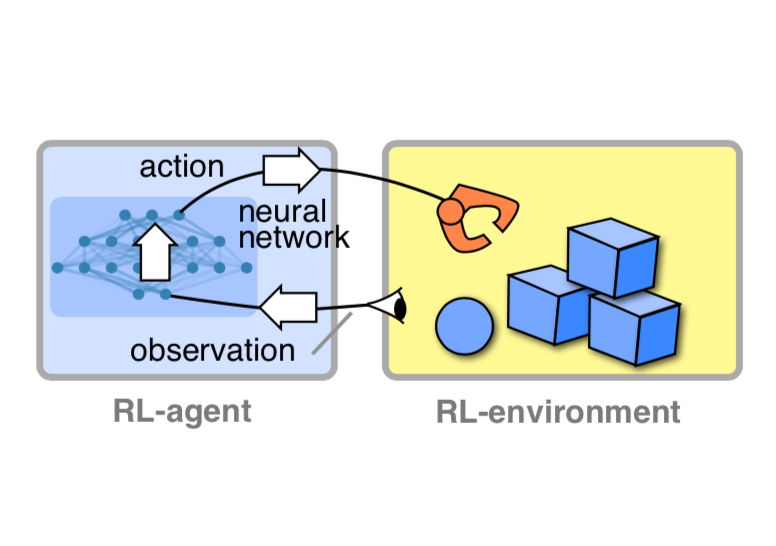
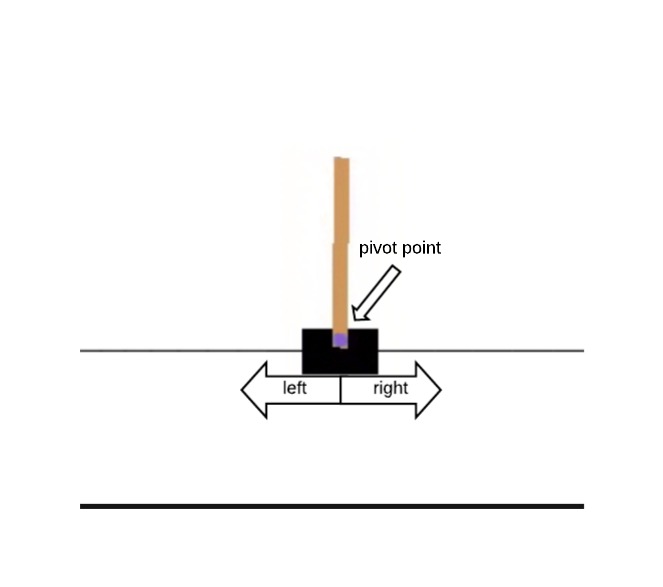
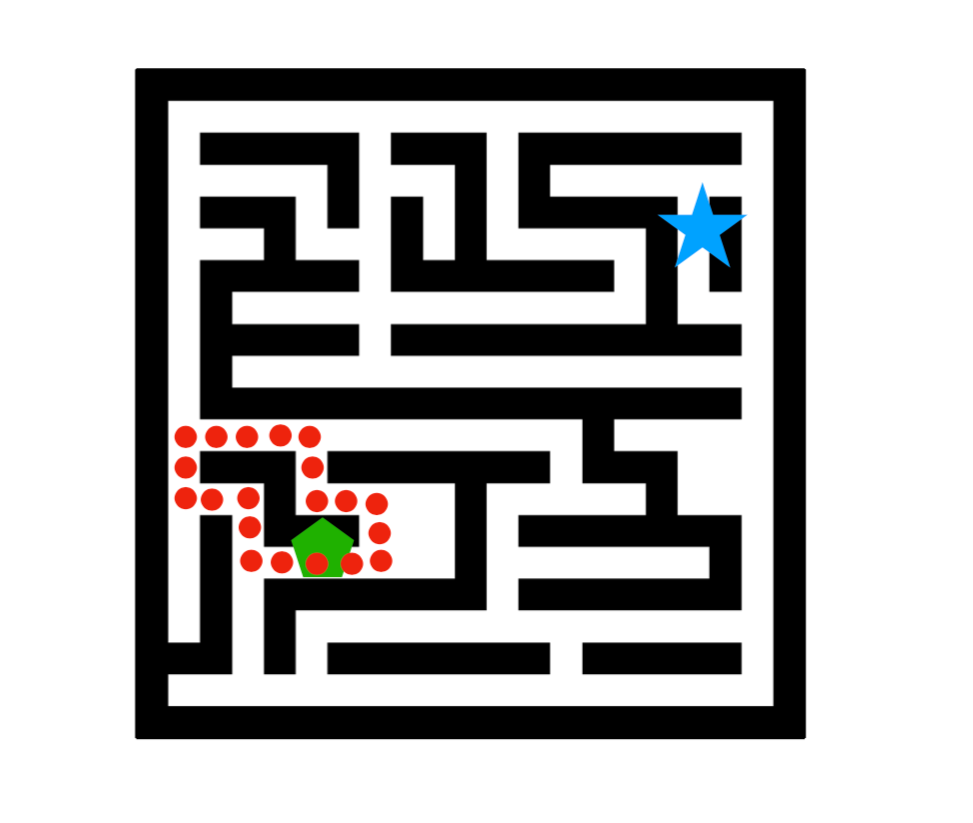
Schedule
Tutorial sessions will take place in the same Lecture Hall of the lectures, from 18.00 to 19.30 on the following dates:
Monday 29.04.19Wednesday 22.05.19Wednesday 12.06.19-
Wednesday 26.06.19 - Wednesday 10.07.19
Change of room: due to an event organized by FAU, the last tutorial session will be held in Lecture Hall A.